Komplexa tal på rektangulär och polär form. Grundläggande geometri och topologi i komplexa planet och på Riemannsfären. Holomorfa, meromorfa och harmoniska funktioner. Konform avbildning. Taylorserier och Laurentserier. Konvergensradie och termvis derivation och integration av potensserier. Klassifikation av singulariteter. Poler och nollställen, argumentprincipen och Rouchés sats. Liouvilles sats med tillämpning. Derivation och integration i komplexa planet. Cauchy-Riemanns ekvationer. Cauchys sats och Cauchys integralformel med följdsatser. Maximumprincipen. Residykalkyl. Tillämpningar inom t ex transformteori, värmeledning och elektricitetslära.
SF1691 Komplex analys 7,5 hp
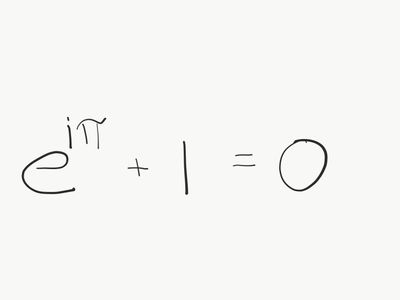
Komplex analys handlar om funktioner av en komplex variabel, speciellt derivator och integraler av sådana funktioner. Holomorfa funktioner, dvs funktioner som är deriverbara i komplex mening, har en mängd intressanta egenskaper och tillämpningar. Det visar sig också att det imaginära talet i är väldigt användbart även i vår reella verklighet. I formeln här intill ser vi de fem viktigaste talen och hur de relaterar till varandra. Information om kursomgången vt 2022 finns på canvas:https://kth.instructure.com/courses/31918
Information per kursomgång
Välj termin och kursomgång för att se aktuell information och mer om kursen, såsom kursplan, studieperiod och anmälningsinformation.
Information för VT 2025 Start 2025-01-14 programstuderande
- Studielokalisering
KTH Campus
- Varaktighet
- 2025-01-14 - 2025-06-02
- Perioder
- P3 (3,7 hp), P4 (3,8 hp)
- Studietakt
25%
- Anmälningskod
60178
- Undervisningsform
Normal Dagtid
- Undervisningsspråk
Svenska
- Kurs-PM
- Kurs-PM är inte publicerat
- Antal platser
Ingen platsbegränsning
- Målgrupp
Sökbar för alla program.
- Planerade schemamoduler
- [object Object]
- Schema
- Del av program
Civilingenjörsutbildning i elektroteknik, åk 2, Villkorligt valfri
Civilingenjörsutbildning i elektroteknik, åk 3, Villkorligt valfri
Civilingenjörsutbildning i teknisk fysik, åk 3, Valfri
Civilingenjörsutbildning i teknisk matematik, åk 2, Villkorligt valfri
Civilingenjörsutbildning i teknisk matematik, åk 3, Valfri
Masterprogram, systemteknik och robotik, åk 1, Rekommenderad
Masterprogram, systemteknik och robotik, åk 1, LDCS, Villkorligt valfri
Masterprogram, systemteknik och robotik, åk 2, Rekommenderad
Masterprogram, systemteknik och robotik, åk 2, LDCS, Villkorligt valfri
Masterprogram, tillämpad matematik och beräkningsmatematik, åk 1, Valfri
Kontakt
Kursplan som PDF
Notera: all information från kursplanen visas i tillgängligt format på denna sida.
Kursplan SF1691 (HT 2019–)Rubriker med innehåll från kursplan SF1691 (HT 2019–) är markerade med en asterisk ( )
Innehåll och lärandemål
Kursinnehåll
Lärandemål
Efter genomgången kurs ska studenten kunna
- Förklara innebörden av grundläggande begrepp, satser och metoder inom de delar av komplex analys som beskrivs av kursinnehållet
- Använda grundläggande begrepp, satser och metoder för att lösa och presentera lösningen av problem inom de delar av komplex analys som beskrivs av kursinnehållet
i syfte att kunna lösa tillämpade problem och att kunna kommunicera med hjälp av matematiskt språk även i andra sammanhang.
För högre betyg ska studenten även kunna
- Förklara hur olika satser och begrepp hänger ihop och härleda samband från givna satser.
Kurslitteratur och förberedelser
Särskild behörighet
Slutförd kurs i SF1626 Flervariabelanalys eller SF1674 Flervariabelanalys.
Utrustning
Ingen information tillagd
Kurslitteratur
Kurslitteratur meddelas senast fyra veckor före kursstart på kursens hemsida.
Examination och slutförande
När kurs inte längre ges har student möjlighet att examineras under ytterligare två läsår.
Betygsskala
A, B, C, D, E, FX, F
Examination
- TEN1 - Tentamen, 7,5 hp, betygsskala: A, B, C, D, E, FX, F
Examinator beslutar, baserat på rekommendation från KTH:s handläggare av stöd till studenter med funktionsnedsättning, om eventuell anpassad examination för studenter med dokumenterad, varaktig funktionsnedsättning.
Examinator får medge annan examinationsform vid omexamination av enstaka studenter.
Examinator beslutar, i samråd med KTH:s samordnare för funktionsnedsättning (Funka), om eventuell anpassad examination för studenter med dokumenterad, varaktig funktionsnedsättning. Examinator får medge annan examinationsform vid omexamination av enstaka studenter.
Möjlighet till komplettering
Ingen information tillagd
Möjlighet till plussning
Ingen information tillagd
Examinator
Etiskt förhållningssätt
- Vid grupparbete har alla i gruppen ansvar för gruppens arbete.
- Vid examination ska varje student ärligt redovisa hjälp som erhållits och källor som använts.
- Vid muntlig examination ska varje student kunna redogöra för hela uppgiften och hela lösningen.
Ytterligare information
Kursrum i Canvas
Registrerade studenter hittar information för genomförande av kursen i kursrummet i Canvas. En länk till kursrummet finns under fliken Studier i Personliga menyn vid kursstart.
Ges av
Huvudområde
Teknik
Utbildningsnivå
Grundnivå
Påbyggnad
Ingen information tillagd