The course is organised in three modules that cover the basics of programming of quantum processors (QPU). The first module covers the fundamentals of quantum computing, including quantum bits and quantum gates and realization in hardware. The second module presents quantum algorithm primitives, such as quantum arithmetic and logic, amplitude amplification, and phase estimation. The third module introduces the main QPU applications, such as quantum search, Shor's factorization algorithm and quantum machine learning.
DD2367 Quantum Computing for Computer Scientists 7.5 credits
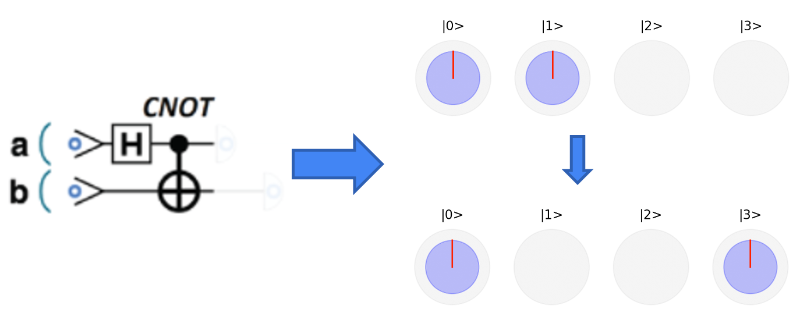
Quantum computing is a new computing paradigm at the intersection of computer science, physics, and mathematics. This course is designed to provide a comprehensive introduction to quantum computing, covering its algorithms, hardware, and programming approaches. The course is suitable for computer scientists of all levels, including those without a formal background in mathematics or physics, and includes programming exercises to reinforce key concepts.
The course is divided into three modules that cover the fundamentals of programming for quantum processors (QPUs). In the first module, you will learn about the basics of quantum computing, including quantum bits and gates and the hardware used to implement them. In the second module, you will be introduced to quantum algorithm primitives, such as quantum arithmetic and logic, amplitude amplification, and phase estimation. Finally, in the third module, you will explore the main QPU applications, including quantum search and Shor's factorization algorithms
Information per course offering
Information for Autumn 2026 quantcs26 programme students
- Course location
KTH Campus
- Duration
- 24 Aug 2026 - 23 Oct 2026
- Periods
Autumn 2026: P1 (7.5 hp)
- Pace of study
50%
- Application code
10842
- Form of study
Normal Daytime
- Language of instruction
English
- Course memo
- Course memo is not published
- Number of places
Min: 8
- Target group
- Open to all master's programmes as long as it can be included in your programme.
- Planned modular schedule
- [object Object]
- Schedule
- Schedule is not published
Contact
Course syllabus as PDF
Please note: all information from the Course syllabus is available on this page in an accessible format.
Course syllabus DD2367 (Autumn 2023–)Content and learning outcomes
Course contents
Intended learning outcomes
After passing the course, the student shall be able to
- describe complex numbers and complex vector spaces for quantum computing
- describe superposition of states, non-locality effects and probabilistic laws
- compare the advantages and disadvantages of classical data processing with quantum computing
- generalize the concept of bit, classical gate, and registers to qubit, quantum gates, and quantum registers
- list, formulate and describe key algorithms in quantum computing
- describe hardware that can realize quantum calculations
in order to design quantum algorithms and programs that can run on current and next-generation quantum computers.
Literature and preparations
Specific prerequisites
Knowledge in algebra and geometry, 7.5 higher education credits, equivalent to completed course SF1624.
Knowledge and skills in programming, 6 credits, equivalent to completed course DD1337/DD1310-DD1319/DD1321/DD1331/DD100N/ID1018.
Literature
Examination and completion
Grading scale
Examination
- LAB1 - Laboratory work, 2.0 credits, grading scale: P, F
- LAB2 - Laborative work, 2.0 credits, grading scale: P, F
- LAB3 - Laborative work, 2.0 credits, grading scale: P, F
- PRO1 - Project work, 1.5 credits, grading scale: A, B, C, D, E, FX, F
Based on recommendation from KTH’s coordinator for disabilities, the examiner will decide how to adapt an examination for students with documented disability.
The examiner may apply another examination format when re-examining individual students.
If the course is discontinued, students may request to be examined during the following two academic years.
Examiner
Ethical approach
- All members of a group are responsible for the group's work.
- In any assessment, every student shall honestly disclose any help received and sources used.
- In an oral assessment, every student shall be able to present and answer questions about the entire assignment and solution.