Dynamisk programmering 2.2
- Frågan var:
Vad är lämpliga dellösningar för en dynamiskprogrammeringsalgoritm för triangelstigsproblemet?
a) V[i,j]=värdet på bästa stigen från toppen ner till elementet \(a_{ij}\)
Dessa dellösningar fungerar för dynamisk programmering, men rekursionen blir ganska krånglig, eftersom den kommer att se olika ut för element inuti triangeln, på vänsterkanten och på högerkanten.
b) V[i,j]=värdet på bästa stigen från toppen till botten som passerar elementet \(a_{ij}\)
Detta fungerar inte som dellösningar eftersom det inte går att bygga en rekursion på dom.
c) V[i,j]=värdet på bästa stigen från elementet \(a_{ij}\) ner till botten
Dessa dellösningar fungerar och ger en enkel rekursion, så c) är att föredra. - Anta att dellösningarna väljs som i c) ovan. Svara sedan på följande två frågor:
- Vad är värdet på maximala triangelstigen uttryckt i V[i,j]?
- Basfallen för rekursionen är V[n,j]=\(a_{nj}\)
Rekursionssteget är V[i,j]=\(a_{ij}\)+ ???
Vad är ???
a) max(V[i-1,j], V[i-1,j+1])
b) max(V[i,j-1], V[i,j+1])
c) max(V[i+1,j], V[i+1,j+1]) - Svaren visas i andra videon.
- Svara på följande färgfråga:
Vilken beräkningsordning är lämplig för den angivna rekursionen för triangelstigsproblemet?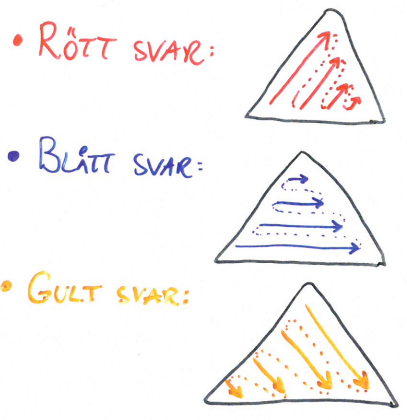
- Klicka här för att se svaret på frågan och nästa video.