Föreläsning 8 Prioritetskö
Läs i boken: kap 5.7, 6.4.5
- Prioritetskö
- Trappa (heap)
- Trappsortering (Heapsort)
- Bästaförstsökning
Prioritetskö
När man poppar en stack får man ut det senast inpushade. När man tar ut något ur en vanlig kö får man tvärtom ut det som legat längst tid i kön. Man skulle kunna se det som att det som stoppas in tidsstämplas och att det påstämplade talet ger prioriteten för uthämtning.
I en prioritetskö stämplas en prioritet på varje objekt som stoppas in och vid uthämtning får man objektet med högst prioritet.
En abstrakt prioritetskö kan ha föjande anrop:
insert(p,x) Stoppa in x med påstämplad prioritet p (oftast ett heltal).
x = delMax() Hämta det som har högst prioritet.
isEmpty() Undersök om prioritetskön är tom.
Om det man vill stoppa in i prioritetskön är ett tal kan man använda talet självt som prioritet och bara skriva insert(x). Hur den då skiljer sej från en stack och från en vanlig kö ser man av följande exempel.
pq.insert(1)
pq.insert(3)
pq.insert(2)
x = pq.delMax() # x blir 3
En kö hade skickat tillbaka det först instoppade talet 1; en stack hade skickat tillbaka det senast instoppade talet, 2; prioritetskön skickar tillbaka det bästa talet, 3. I denna prioritetskö betraktar vi största talet som bäst - vi har en så kallad maxprioritetskö. Det finns förstås också minprioritetsköer, där det minsta talet betraktas som bäst.
Prioritetsköer har många användningar. Man kan tänka sej en auktion där budgivarna stoppar in sina bud i en maxprioritetskö och auktionsförrättaren efter "första, andra, tredje" gör pq.delMax() för att få reda på det vinnande budet. För att hen ska veta vem som lagt detta bud behövs förstås båda parametrarna ipq.insert(p,x).
pq.insert(bud,person) #person är ett objekt med budgivarens namn och bud
winner = pq.delMax() #budgivaren med högst bud
Trappa
Den bästa implementationen av en prioritetskö är en trappa, (eng heap), som är en lista tolkad som binärträd.
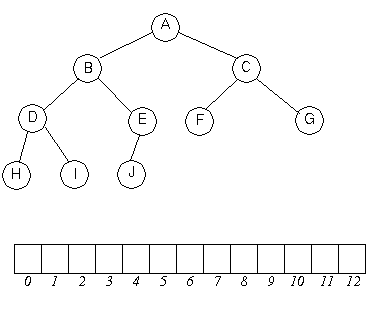
Roten är tab[1], dess båda barn är tab[2] och tab[3] osv. Vi använder inte tab[0]. Allmänt gäller att tab[i] har barnen tab[2*i] och tab[2*i+1]. Trappvillkoret är att föräldern är bäst, dvs varje tal ligger på två sämre tal.
Ett nytt tal läggs alltid in sist i trappan. Om trappvillkoret inte blir uppfyllt, dvs om det är större än sin förälder, byter förälder och barn plats och så fortgår det tills villkoret uppfyllts. Det här kallas upptrappning och kan i värsta fall föra det nya talet hela vägen upp till toppen, alltså tab[1].
Man plockar alltid ut det översta talet ur trappan och fyller igen tomrummet med det sista talet i trappan. Då är inte trappvillkoret uppfyllt, så man får byta talet och dess största barn. Denna nedtrappning upprepas tills villkoret åter gäller.
Både insert och delMax har komplexitet log N om trappan har N element.
Här följer en rudimentär implementation av en max-heap:
class HeapNode:
def __init__(self, data, priority):
"""data är det objekt vi vill lagra
priority är nyckelvärdet som används för att jämföra objekten"""
self.data = data
self.priority = priority
class Heap:
# En max-heap
def __init__(self):
"""Skapar en lista där vi använder element 1..maxsize"""
self.maxsize = 32
self.tab = (maxsize+1)*[None]
self.size = 0
def isEmpty(self):
"""Returnerar True om heapen är tom, False annars"""
return self.size == 0
def isFull(self):
"""Returnerar True om heapen är full, False annars"""
return self.size == self.maxsize
def insert(self, data, priority):
"""Lägger in nya data med nyckeln priority i heapen"""
if not self.isFull():
self.size += 1
self.tab[self.size] = HeapNode(data, priority)
i = self.size
while i > 1 and self.tab[i//2].priority < self.tab[i].priority:
self.tab[i//2], self.tab[i] = self.tab[i], self.tab[i//2]
i = i//2
def delMax(self):
"""Hämtar det största (översta) objektet ur heapen"""
if not self.isEmpty():
data = self.tab[1]
self.tab[1] = self.tab[self.size]
self.size -= 1
i = 1
while i <= self.size//2:
maxi = self.maxindex(i)
if self.tab[i].priority < self.tab[maxi].priority:
self.tab[i],self.tab[maxi] = self.tab[maxi], self.tab[i]
i = maxi
return data.data
else:
return None
def maxindex(self, i):
"""Returnerar index för det största barnet"""
if 2*i+1 > self.size:
return 2*i
if self.tab[2*i].priority > self.tab[2*i+1].priority:
return 2*i
else:
return 2*i+1
Heapsort
Om man stoppar in N tal i en trappa och sedan hämtar ut dom ett efter ett får man dom sorterade. Komplexiteten för denna heapsort blir O(N log N), alltså av lika god storleksordning som quicksort. Visserligen är quicksort lite snabbare, men heapsort har inte quicksorts dåliga värstafallsbeteende. och så kan ju en heap användas till andra saker än sortering också.
heap = Heap()
for word in open("folksagor.txt").read().split():
heap.insert(word, word)
while not heap.isempty():
print heap.delMax()
Bästaförstsökning
Labb 4 behandlar problemet att finna kortaste vägen från FAN till GUD. Man har då ett problemträd med FAN som stamfar/urmoder, på nivån därunder barnen MAN, FIN, FAT osv, på nästa nivå fans barnbarn osv. Om man lägger barnen i en kö kommer man att gå igenom problemträdet nivå för nivå, alltså breddenförst. Om man byter kön mot en stack blir sökningen djupetförst. Med en prioritetskö får man bästaförstsökning, dvs det mest lovande barnet prioriteras och får föda barn.
Det här är exempel på en girig algoritm, där man i varje steg väljer den väg som verkar bäst för stunden, utan att reflektera över vad konsekvenserna blir i längden. Ofta ger giriga algoritmer inte den bästa lösningen, men i just det här fallet fungerar det faktiskt! Algoritmen kallas Dijkstra's algoritm (efter den holländske datalogen Edsger W. Dijkstra) och att den fungerar bevisas i fortsättningskursen DD1352 Algoritmer, datastrukturer och komplexitet.
Exempel 1: Sök billigaste transport från Teknis till Honolulu. All världens resprislistor finns tillgängliga.
Problemträdets objekt innehåller en plats, ett pris och en förälderpekare. Överst i trädet står Teknis med priset noll. Barnen är alla platser man kan komma till med en transport och priset, till exempelT-centralen, 20.00. Man söker en Honoluluobjekt i problemträdet. Med breddenförstsökning får man den resa som har så få transportsteg som möjligt.
Med bästaförstsökning får man den billigaste resan.
Exempel 2: Sök effektivaste processen för att framställa en önskad substans från en given substans. All världens kemiska reaktioner finns tillgängliga med uppgift om utbytet i procent.
Problemträdets objekt innehåller substansnamn och procenttal. Överst i trädet står utgångssubstansen med procenttalet 100. Barnen är alla substanser man kan framställa med en reaktion och utbytet, till exempel C2H5OH, 96%.
Med en max-prioritetskö får man fram den effektivaste process som leder till målet.