Föreläsning 4 Binära träd

Idag:

  • Allmänna träd
  • Binära sökträd
  • Rekursiva tankar för binärträd

Allmänna träd

Stack och kö är två viktiga datastrukturer man kan bygga av objekt, där varje objekt refererar till ett annat objekt. 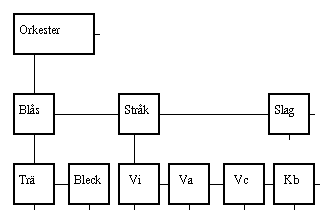TRÄD Med två referenser i varje objekt kan man bygga träd, till exempel ett som beskriver en symfoniorkesters sammansättning.
Här har objekten följande utseende.

    class Node:
       def __init__(self, value):
          self.value = value
          self.down = None
          self.right = None

All systematisk uppdelning kan beskrivas med liknande träd, till exempel ett bokverks uppdelning i delar, kapitel, sektioner osv. Man kan också tänka sej det som ett släktträd och då kallas ofta down-referensen för firstChild och right-referensen för nextSibling. Det räcker med två referenser i varje nod, oavsett hur stora barnaskarorna är.

Användningsområden

Trädstrukturer är hierarkiska och sådana datastrukturer är mycket vanliga. Några exempel:

  • Filsystemet använder träd (man kan ha underkataloger i underkataloger).
  • När du kör ditt Pythonprogram byggs ett syntaxträd upp för programmet.
  • Databaser använder träd för att få snabb sökning.
  • Schackprogram använder träd för att gå igenom resultaten av möjliga drag.
  • Vid datakomprimering kan man använda träd för att få fram en optimal kod (Huffmanträd, kommer på komprimeringsföreläsningen).

BINÄRTRÄD

Definitioner

  • Noder är de objekt som trädet är uppbyggt av. De innehåller data och pekare.
  • Rot är den översta noden i trädet. Den pekas inte ut av någon annan nod.
  • Barn till en nod är de som pekas ut av noden.
  • Förälder är noden ovanför i trädet.
  • Syskon har samma förälder.
  • Löv är en nod vars bägge pekare är None.
  • Delträd definieras så här: En godtycklig nod i trädet kan ses som en rot, och den , tillsammans med alla noder under den (barn, barnbarn osv.) bildar ett delträd.
  • Nivå är det antal steg från roten noden befinner sig. Roten är på nivå noll.
  • Höjd är den maximala nivån som nån av trädets noder befinner sig på.
  • Balanserat är binärträdet om skillnaden i höjd mellan höger och vänster delträd till varje nod är noll eller ett.
  • Fullt är binärträdet om alla noder utom löven har exakt två barn, och alla löv är på samma nivå.

Binärträd

När man programmerar binärträd brukar man använda noder, som i en länkad lista, men med två pekare: en åt vänster och en åt höger:

    class Node:
       def __init__(self, value):
          self.value = value
          self.left = None
          self.right = None

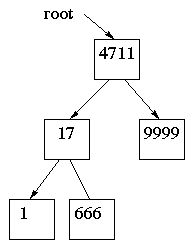
Man når trädet genom variabeln root som pekar på den översta noden (datalogiska träd har roten uppåt). Rotnodens vänsterpekare pekar på ett mindre binärträd och högerpekaren på ett annat mindre binärträd.

Antalet nivåer i trädet avgör hur många noder det kan innehålla. Ett fullt träd med k nivåer innehåller 2k - 1 noder. Exempel: k=3 i vår bild ger högst 7 noder (det finns plats för två till under 9999). Man kan också säga att ett balanserat träd med n noder har cirka log n nivåer.





Binära sökträd


I vårt exempelträd ligger små tal till vänster och stora tal till höger. När det är på det sättet har man ett binärt sökträd, så kallat eftersom det går så snabbt att söka reda på en nod i trädet. Låt oss säga att vi söker efter 666. Vår algoritm blir följande


    

  • Kolla först rottalet.
    • 

  • Om talet är 666 har vi funnit vad vi söker.
    • 

  • Om talet är större än 666 letar vi vidare efter 666 i vänsterträdet.
    • 

  • Om det är mindre än 666 letar vi vidare i högerträdet.
    • 

  • ...men om vi når en None-referens finns inte 666 i sökträdet.
    • 



Algoritmer som går igenom varje nod i trädet (t ex utskrift) har tidskomplexitet O(n). Men sökningen tar bara O(logn) om trädet är balanserat, därför att vi som mest går igenom trädets höjd.


    def finns(p,value):
        letar = True
        while letar:
            if p == None: 
                return False
            if value == p.value: 
                return True
            if value < p.value: 
                p = p.left
            if value > p.value: 
                p = p.right





Rekursivt listexempel


Vi tänker oss en länkad lista av noder, där varje nod innehåller ett värde och en next-pekare.
 Fråga: Hur många noder finns i listan? 
 Rekursivt svar: En nod mer än i listan under översta noden.  
 Basfall: En tom lista har noll noder.


    def antal(p):
        if p == None: 
            return 0
	else:        
            return 1 + antal(p.next)



Anropet antal(p) ger nu rätt svar!




Rekursiva tankar för binärträd


Fråga: Hur många noder finns i binärträdet? 
 Rekursivt svar: En nod mer än i vänsterträdet och högerträdet tillsammans
Basfall: Ett tomt träd har noll noder.


    def antal(p):
        if p == None: 
            return 0
        else:
            return 1 + antal(p.left) + antal(p.right)



Anropet antal(root) ger nu rätt svar!




Sökning i ett binärt sökträd kan implementeras rekursivt om man låter anropet finns(p,value) returnera True ifall ordet finns i det delträd där p är rot.


    def finns(p,value):
        if p == None: 
            return False
        if value == p.value: 
            return True
        if value < p.value: 
            return finns(p.left,value)
        if value > p.value: 
            return finns(p.right,value)



Den här funktionen kan du använda i labb 3! 
 Där ska du göra en klass som fungerar som ett abstrakt binärt sökträd med operationer för att stoppa in ett element, söka efter ett värde och skriva ut alla värden.


Utskrift av binärträd: inorder, preorder, postorder


Om man ska skriva ut alla talen i trädet vill man oftast göra det i så kallad inordning (eng. inorder), dvs från vänster till höger. 
 Fråga: Hur skriver man ut trädet i inordning? 
 Rekursivt svar: Först skriver man ut vänsterträdet, sedan rottalet, sist högerträdet.
 Basfall: Ett tomt träd skriver man inte ut.



 Följande funktion gör att write(root) skriver ut 1 17 666 4711 9999 för vårt träd.


#Inordning
    def inorder(p):
        if p != None:
            inorder(p.left)
            print(p.value)
            inorder(p.right)



Om man kastar om dom tre sista satserna får man ändå ut alla talen på skärmen men i andra ordningar. Preordning (eng. preorder) innebär att rottalet skrivs först, sedan vänsterträdet och sist högerträdet. I vårt exempel blir ordningen 4711   17   1   666   9999.


Om vi återgår till orkesterträdet kan vi se att preordning faktiskt ger vettigare utskrift. Så här blir koden i det fallet.


#Preordning     
    def preorder(p):
        if p != None:
            print(p.value)
            preorder(p.down)
            preorder(p.right)



Utskriften blir då den naturliga. Om vi för tydlighets skull använder indragning av orden på lägre nivå blir utskriften


    Orkester              
        Blås
            Trä
            Bleck
        Stråk
            Vi
            Va
            Vc
            Kb
        Slag



(Hur gör man för att få dessa indragningar?)


Slutligen kan man skriva ut i postordning (eng. postorder) och det innebär att vänsterträdet skrivs först, sedan högerträdet och sist roten. Det ger 1   666   17   9999   4711 i vårt exempel.



    
  


  
  
  

  

  

        

      

      
    

    





  

  
  



  

    Feedback
    
    Nyheter