Föreläsning 12 Komprimering
Komprimering
- Läs i boken: kap 7.5
- Tal i bas 2, 8 och 16
- Filformat (.txt .doc .jpg etc)
- Storleksordningar data
- Komprimering
- Följdlängdskodning (run-length encoding)
- Huffmankodning
- Lempel-Ziv-kodning
- Entropi
- Komprimering av bilder
- Komprimering av rörliga bilder
- Komprimering av ljud
- Felkorrektion
- Image compression for a small satellite: lessons learned
Binära tal (och andra baser)
Till vardags använder vi decimala talsystemet med tio siffror: 0-9. Andra talsystem finns, t ex binära tal (två siffror: 0-1), oktala tal (åtta siffror: 0-7) och hexadecimala tal (sexton siffror:0-F).
| Decimalt | Binärt | Oktalt | Hexadecimalt |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| 18 | 10010 | 22 | 12 |
| 19 | 10011 | 23 | 13 |
| 20 | 10100 | 24 | 14 |
Det är extra enkelt att konvertera binära tal till oktala resp hexadecimala: tre binära siffror ger en oktal siffra, och fyra binära siffror ger en hexadecimal siffra.
I python kan man skriva binära, oktala och hexadecimala tal direkt, med prefixet 0b,0o respektive 0x.
Minnesadresser skrivs ut som hexadecimala tal, exempel:
<__main__.MittEgetObjekt instance at 0x7f7cf8cb22d8>
Komprimering
Komprimering innebär att man använder någon metod för att minska storleken på en fil. Vi skiljer mellan förlustfri komprimering (non-lossy compression) där det går att dekomprimera för att få tillbaka filen i ursprungligt skick och förstörande komprimering (lossy compression) där man tar bort data. Att det går att komprimera utan att förstöra en fil beror på att filer oftast har redundans, dvs innehåller mer än nödvändigt.
Följdlängdskodning - RLE
I följdlängdskodning, förkortat RLE (Run-Length-Encoding), utnyttjar man att en följd av likadana tecken kan lagras med antal istället för att skrivas ut.
ÅÅÅÅH! JAAAAAAA! AAAAAAAAAAAAH.
Vi ersätter följderna av Å och A med antalet följt av det upprepade tecknet:
4ÅH! J7A! 12AH.
Men om grundtexten innehåller siffror blir det svårtolkat. Därför väljer vi ett bryttecken, t ex §, som vi är säkra på inte kommer att förekomma i texten.
§4ÅH! J§7A! §12AH.
Algoritmen blir enkel, men tyvärr inte så användbar för textkomprimering eftersom de flesta texter inte innehåller längre följder av samma tecken.
Huffmankodning
Om vi vet hur vanliga olika tecken är i texten kan vi ställa upp en tabell där vi för varje tecken kan ange sannolikheten för att ett visst tecken ska dyka upp. I David A. Huffmans metod kodar man varje tecken med ett binärt tal, där vanligare tecken får kortare koder. Algoritmen som beräknar vilket tecken som ska få vilken binär kod går ut på att man ritar upp ett binärt träd, där varje tecken ses som ett löv. Sedan numrerar man trädets grenar med 0 och 1 och följer trädet från roten ut till varje löv för att se koderna.
- Sortera tecknen som ska kodas i stigande sannolikhetsordning.
- Rita grenar från de två tecken som har lägst sannolikhet och låtsas att vi har ett nytt tecken med sannolikhet som är summan av deras sannolikheter. Numrera ena grenen med 0 och andra med 1.
- Upprepa punkt 2 tills alla tecken kommit med. Roten bör få sannolikhet 1.
- Börja från roten och följ grenarna ut till ett löv. Samla nollor och ettor på vägen - dessa ger koden för lövets tecken.
Vi illustrerar algoritmen med ett exempel. En genomgång av skräcklitteraturen ger följande frekvenstabell:
| Huffmankod | Tecken | Sannolikhet |
| G | 0.05 | |
| R | 0.05 | |
| ! | 0.1 | |
| . | 0.15 | |
| A | 0.15 | |
| H | 0.2 | |
| I | 0.3 |
Texten HAHA!IIIIIIH!AHRG... skulle alltså kodas som
01 101 01 101 001 11 11 11 11 11 11 01 001 101 01 0001 0000 100 100 100
Huffmankodning är en statistisk metod.
Lempel-Ziv
Alla texter följer inte statistiken. Här följer ett utdrag ur romanen Gadsby av Ernest Vincent Wright (1872-1939).
IF YOUTH, THROUGHOUT all history, had had a champion to stand up for it; to show a doubting world that a child can think; and, possibly, do it practically; you wouldn't constantly run across folks today who claim that ''a child don't know anything.'' A child's brain starts functioning at birth; and has, amongst its many infant convolutions, thousands of dormant atoms, into which God has put a mystic possibility for noticing an adult's act, and figuring out its purport.
Jacob Ziv och Abraham Lempel uppfann en förutsättningslös metod som anpassar sig till indata. Principen är att man går igenom filen och bygger en ordlista som används för kodningen. Lempel-Ziv finns i ett otal olika varianter: LZ77, LZSS, LZFG, LZW, LZMW, LZAP, LZY, LZP, osv. Så här fungerar LZW (en variant gjord av T. Welch):
- Läs in tecken för tecken och slå ihop till en sträng s.
- Fortsätt på det viset så länge som strängen redan finns med i ordlistan.
- Så småningom får vi en sträng som inte finns i ordlistan (s finns med men inte s+c).
- Skriv då ut koden för strängen s, skriv ut tecknet c, och lägg in s+c i ordlistan.
def lzw(text):
table = Table()
q = Queue()
for c in text: # spara texten tecken för tecken i en kö
q.enqueue(c)
s = ""
kodtext = "" # här sparas det kodade meddelandet
while not q.isEmpty():
print(table)
c = q.dequeue()
if table.exists(s+c):
s = s + c
else:
kodtext += str(table.code(s)) + c
table.add(s + c)
s = ""
if not s == "":
kodtext += str(table.code(s))
return kodtext
Klassen Table (som används för ordlistan) är tänkt att vara en datastruktur där man kan stoppa in strängar med add(), kolla om en sträng finns med exists(), och få ut en kod för en given sträng med code().
LZ-komprimering används i många komprimeringsprogram, t ex compress, zip, WinZip och GZip (här i kombination med Huffmankodning).
Exempel: Använd LZW-algoritmen ovan för att komprimera NÄSSNUVSNORSNOK
Om vi använder en vektor som tabell och för enkelhets skull kodar strängarna med vektorindex får vi tabellen:
| code | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| sträng | "N" | "Ä" | "S" | "SN" | "U" | "V" | "SNO" | "R" | "SNOK" |
och det komprimerade ordet blir: NÄS2NUV3OR6K
Entropi
Hur mycket kan man komprimera utan att förlora information?
Om det var möjligt att komprimera hur mycket som helst skulle vi kunna få ner varje fil till en bit, men det kan vi uppenbarligen inte. Det finns alltså en undre gräns för hur kompakt man kan få en fil med förlustfri komprimering. Om man känner till sannolikheten för varje tecken som ska kodas (som i skräckexemplet ovan) kan man beräkna entropin som ger en undre gräns för medellängden hos en kod.
Anta att vi har en teckenmängd m1, m2,...,mn (t ex alfabetet) och att sannolikheten för att tecknet mi ska förekomma är P(mi).
Då är L(mi)=-log(P(mi)) minimilängden för ett kodord för tecknet mi och
Lmedel = P(m1)*L(m1) + ... + P(mn)*L(mn)
medellängden för koderna (entropin).
Komprimering av bilder
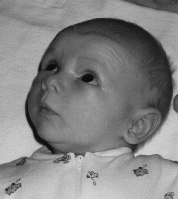
Det är vanligt att varje bildpunkt (pixel) i en färgbild representeras med ett 24-bitars binärt tal (vilket ger oss åtta bitar för vardera rött, grönt resp blått). Då tar en färgbild 100x100 pixlar 24000 bitar, dvs 24 kB och en bild som täcker en 600x800-skärm tar 11.5 MB.
 |
 |
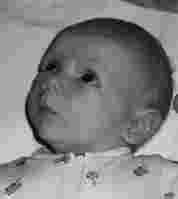 |
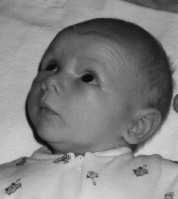
| GIF 24 kB | JPEG 3 kB | JPEG 1.5 kB |
Vilken redundans kan finnas i en bild? Vissa färger kanske är vanligare, så att vi kan använda Huffmankodning för att få kortare koder för dessa. I foton är närliggande pixlar ofta lika (blå himmel t ex), likaså i streckteckningar och grafer (bara svarta och vita pixlar). Där kan man använda RLE genom att räkna antal vita resp svarta pixlar i följd. Även varianter av LZW kan användas - då innehåller tabellen pixelinfo istället för strängar! Vi kan också använda förstörande komprimering för att ta bort information som ögat ändå inte ser.
GIF (Graphics Interchange Format) är ett filformat för bilder där färgkodningen görs med 8 bitar, dvs man får 28=256 färger. Sen används en variant av LZW för att komprimera. Den komprimeringen är förlustfri och storleken minskas med ungefär faktorn 4.
JPEG (Joint Photographic Experts Group) är bättre för foton och andra bilder där närliggande pixlar har liknande färger. Färgbilder delas upp i en belysningsdel och en färgdel, där färgdelen komprimeras med förstörande komprimering eftersom ögat är mindre känsligt för färgförändringar. Sen används en kombination av RLE och Huffmankodning för att koda grupper av pixlar. Komprimeringsgraden är parameter till algoritmen, så man kan bestämma själv hur hårt man vill komprimera. Färgkodningen görs med 24 bitar, dvs 224 (nästan 17 miljoner) färger.
Komprimering av rörliga bilder
En videofil innehåller massor av bilder och dessutom ljud så det är extra viktigt att kunna komprimera såna. Dekomprimeringen måste gå snabbt om man direkt ska kunna se filmen i realtid. Det mest kända formatet för rörliga bilder är MPEG (Moving Picture Experts Group). MPEG är egentligen en samling standarder för kombinationer av ljud och video.
Komprimeringen av video-delen kan delas upp i bildkomprimering av varje enskild bildruta och tidskomprimering där man utnyttjar likhet mellan på varandra följande bilder.
För bildkomprimeringen används i regel JPEG. För tidskomprimeringen finns ett antal olika metoder:
- Koda likheter (att en del av bilden ser likadan ut som i förra rutan).
- Koda förskjutningar (att en del av bilden har förskjutits sen förra rutan).
- Koda skillnaden mellan två bildrutor.
- Koda förväntad rörelse.
Tidskomprimeringen kan göra det knepigare att redigera filmen.
Komprimering av ljud
Digital lagring av ljud innebär automatiskt en komprimering eftersom vi samplar en analog ljudkurva i ett ändligt antal punkter. Vidare komprimering av digitala ljudfiler kan göras med RLE eller Huffmankodning. Däremot fungerar inte LZ-metoderna särskilt bra, eftersom de bygger på att man hittar upprepningar. Och även om t ex ett musikstycke upprepar sig är det osannolikt att samma upprepningar skulle återfinnas i ljudfilen efter samplingen.
När det gäller ljud kan man också använda förstörande metoder Två exempel på sådana är tystnadskomprimering där man ersätter mycket svaga ljud med tystnad och companding där man minskar ordlängden för varje ljudpunkt (t ex från 16 till 12 bitar).
MP3 (MPEG Audio Layer-3 encoding) använder en kombination av tekniker där man utnyttjar en modell av den mänskliga hörseln samt Huffmankodning.
Video om digitala medier
Felkorrektion
Vill man gardera sig mot fel kan man lägga till redundans (motsatsen till komprimering). Det finns många olika sätt att göra det på, här följer några exempel:
- Kontrollsiffra (t ex sista siffran i ett personnummer).
- Skicka kopior av hela meddelandet, minst tre behövs om man ska kunna korrigera.
- Paritetsbitar, att man lägger till en etta eller nolla till ett binärt tal för att göra det udda. Ett jämnt tal innebär att nån bit är fel.
- Hammingavstånd: Lägg till så många extrabitar till koden så att varje enbitsfel ger ett kodord som skiljer sig i en bit från det korrumperade kodordet, men i flera bitar från alla övriga kodord. Två kodord har Hammingavstånd d om dom skiljer sig åt i d bitar.
En kod har Hammingavstånd d om alla kodord är minst d ifrån varann. Givet koderna nedan - hur ska vi tolka meddelandet 10010 01110 10101 ?
| A | 01011 | |
| F | 10010 | |
| I | 01100 | |
| N | 10101 |