Föreläsning 9 Automater och textsökning
Automater, textsökning, KMP
- Läs i boken: kap 7.6
- Automater
- Textsökning
- KMP-automat
- Boyer-Moore
- Rabin-Karp
- Sökning på webben
- Reguljära uttryck
- Modellering av grafiska gränssnitt
Automater
En portkodsautomat med nio knappar kan se ut så här:
| A | B | C | ||||||||
| D | E | F | ||||||||
| G | H | I |
Anta att den rätta knappföljden är DEG. Då har automaten fyra olika tillstånd:
- Starttillstånd.
- Knapptryckning D har just gjorts.
- Knapptryckningarna DE har just gjorts.
- Knapptryckningarna DEG har just gjorts. Låset öppnas.
När automaten är i ett visst tillstånd och en viss knapp trycks ner övergår den i ett nytt tillstånd, och det kan beskrivas med en övergångsmatris:
A B C D E F G H
1 1 1 1 2 1 1 1 1 Exempel: Om automaten är i tillstånd 3
2 1 1 1 2 3 1 1 1 och knapp D trycks ner övergår den till
3 1 1 1 2 1 1 4 1 tillstånd 2
Man kan också rita en graf med fyra noder (som representerar tillstånden) och en massa bokstavsmärkta pilar (som visar vilka övergångar som finns).
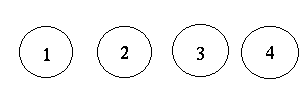
Här är några fler exempel på vad automater kan användas till:
- Söka efter ett ord i en text (se KMP-automat nedan).
- Tolka reguljära uttryck.
- Beskriva grafiska gränssnitt.
- Kompilatorns/interpretatorns analys av ditt program (se föreläsning om syntax).
- Komprimering.
- Morfologisk analys av ord (t ex o-ut-trött-lig-a).
Textsökning
Samma automat kan användas för textsökning, till exempel för att söka efter GUD i bibeln. Bokstav efter bokstav läses och automaten övergår i olika tillstånd. När fjärde tillståndet uppnås har man funnit GUD. Datalogins fader, Donald Knuth, uppfann tillsammans med Vaughan Pratt en enkel metod att konstruera och beskriva automaten. James H. Morris kom på samma sak oberoende av dom två! Därför kallar vi automaten KMP-automat. En KMP-automat har bara en framåtpil och en bakåtpil från varje tillstånd. Så här blir den:
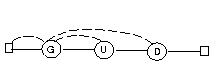
Ett nolltillstånd har skjutits in längst till vänster. Automaten startar emellertid i tillstånd 1, som har ett G i noden. Den tjuvtittar på första bokstaven i bibeln, och om det är ett G läser den G-et och går till höger. Annars följer den bakåtpilen utan att glufsa bokstaven. I nolltillståndet glufsar den alltid en bokstav och går till höger. Koden blir i princip så här, om vi först antar att bokstäverna lästs in i en kö, som har en extra metod peek(), med vilken man kan tjuvtitta på första bokstaven.
i = 1 # starttillståndet
while i < 4:
if i == 0 or q.peek() == sokord[i]:
i = i+1
q.get()
else:
i = next[i];
Här är sokord[i] i-te bokstaven i det sökta ordet och next[i] det tillstånd man backar till från tillstånd i. Nextvektorn (bakåtpilarna) i vårt exempel blir
| i | next[i] |
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
Om vi i stället söker efter ADAM i bibeln blir KMP-automaten så här:
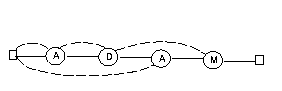
Nextvektorn för ADAM blir alltså den här:
| i | next[i] |
| 1 | 0 |
| 2 | 1 |
| 3 | 0 |
| 4 | 2 |
För GUD gick bakåtpilen från tillstånd 3 till tillstånd 1, men här vore meningslöst att två gånger i rad kolla om bokstaven är A. Bakåtpilen från tillstånd 4 till tillstånd 2 kräver också en förklaring. Om vi har sett ADA och nästa bokstav inte är ett M kan vi i alla fall hoppas att det A vi just sett ska vara början på ADAM. Därför backar vi till tillstånd 2 och undersöker om det möjligen kommer ett D. Reglerna för hur nextvektorn bildas kan sammanfattas så här:
- next[1]=0.
- Annars är next[i]=1 om ordet inte upprepar sej.
- ...men om de j senaste bokstäverna vi sett bildar början på sökordet sätts next[i]=j+1.
- ...men om bokstav j+1 är samma som bokstav i sätts i stället next[i]=next[j+1].
Kom ihåg att nextvektorn bara behövs när det kommer ett dåligt tecken.
Ett annat exempel om man söker efter IRANIRAQ
| ← | ← | ← | ← | ← | ← | ← | |||
| ↓ | ↑ | ↑ | ↑ | ↑ | ↑ | ||||
| o | I | R | A | N | I | R | A | Q | |
| ↑ | ← | ↓ | ← | ← | ← | ↓↑ | ← | ← | ↓ |
Nextvektorn :
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 4 |
Tips för tentatal där nextvektor ska anges. Börja med att leta upprepningar av begynnelseordföljder, i det här fallet IRA och sätt index på tecknet efter, i det här fallet Q -> 4. Leta sedan begynnelsebokstaven, den går alltid till noll. Sätt därefter ettor resterande platser i next-vektorn.
i vissa böcker går begynnelsebokstaven till ett. Då förskjuts siffrorna ett steg och räknas som rätt på tentan).
Om den sträng vi söker efter är m tecken lång och texten vi söker i är n tecken lång kräver KMP-sökning aldrig mer änn+m teckenjämförelser och är alltsåO(n+m). Metoden går igenom texten tecken för tecken - man kan alltså läsa ett tecken i taget t ex från en fil vilket är praktiskt om texten är stor.
Boyer-Moore
Då hela texten vi söker i finns i en lista kan man istället använda Boyer-Moores metod. Den börjar med att försöka matcha sista tecknet i söksträngen, som är m tecken lång. Om motsvarande tecken i texten inte alls förekommer i söksträngen hoppar den fram m steg, annars flyttar den fram så att tecknet i texten passar ihop med sista förekomsten i söksträngen.
Exempel: Vi söker efter TILDA i texten MEN MILDA MATILDA.
MEN MILDA MATILDA
TILDA
TILDA
TILDA
TILDA
MEN MILDA MATILDA
Boyer-Moore är O(n+m) i värsta fallet, men ca n/m steg om texten vi söker i består av många fler tecken än dom som ingår i söksträngen, så att vi oftast kan hoppa fram m steg.
När du skriver Ctrl-S för att söka efter en sträng i Emacs är det Boyer-Moore som används.
J Strother Moores egen animation av Boyer-Moore.
Rabin-Karp
Beräknar en hashfunktion för söksträngen och jämför med hashfunktionen beräknad för alla avsnitt av längden m i texten. Låt oss söka efter "TILDA" i texten "MEN MILDA MATILDA". Med Pythons hashfunktion hash() % 17 får vi hash(TILDA)=16
hash(MEN M) = 6
hash(EN MI) = 15
hash(N MIL) = 9
hash( MILD) = 1
hash(MILDA) = 7
hash(ILDA ) = 13
hash(LDA M) = 15
hash(DA MA) = 12
hash(A MAT) = 0
hash( MATI) = 5
hash(MATIL) = 12
hash(ATILD) = 3
hash(TILDA) = 16
Komplexiteten är O(nm) i värsta fallet. I flera praktiska tillämpningar ör den O(n+m) men det förutsätter att man kan utnyttja det förra hashvärdet för att räkna ut nästa hashvärde t.ex. om man använder en produktsumma för att räkna ut hashvärdet.
bas = 129 # storleken på alfabetet - talet 129 är godtyckligt valt
primtal = 2147483647 # = 2^31 -1 ett primtal mindre än 2^32
# så att hashtalet ryms i en 32-bitars int
# vilket är optimalt på ett 32-bitars OS
sokt = "ngot vi letar i en text" # 23 bokstäver lång söksträng
sokhash = 0
for tkn in sokt:
sokhash = ( bas*sokhash + ord(tkn) ) % primtal
På samma sätt räknar man ut texthash för de 23 första tecknena i texten. Det första tecknet har multiplicerats med bas 22 gånger (23 -1).
Om sokt inte matchar kan man i princip räkna ut nästa hashvärde för texthash genom att lägga till värdet på nästa tecken och dra ifrån bas^22 multiplicerat med teckenvärdet som ska bort.
När hashvärdena matchar måste man fortfarande jämföra sökträngen och textsträngen tecken för tecken.
Sökning på webben
När man använder en sökmotor, t ex Google, för att hitta webbsidor som innehåller ett visst ord skulle alla ovanstående metoder bli för tidsödande. Där slår man istället upp ordet i ett index som skapats i förväg. Hur det fungerar kan man läsa mer om i kursen DD2418, Språkteknologi.
Reguljära uttryck
Om man t ex skulle vilja söka efter lab1, Lab2, eller labb3 så kan man använda ett reguljärt uttryck för att beskriva söksträngen. Ett reguljärt uttryck består av tecken och metatecken som tillsammans utgör ett sökmönster. Metatecken (t ex * och +) har särskild innebörd. Här följer några regler:
- a* matchar noll eller flera a:n
- a+ matchar ett eller flera a:n
- a? matchar ett eller inget a
- . matchar alla tecken utom radslut
- [a-zA-Z] matchar alla engelska bokstäver
- [abc] matchar a, b eller c
- [^abc] matchar vilket tecken som helst utom a, b eller c
- X|Y matchar uttrycket X eller uttrycket Y
- \. matchar en punkt. Tecknet "\" används för att rädda det efterföljande tecknet från att tolkas som ett metatecken.
- (ab) skapar en grupp. T ex matchar (ab)+ ett eller flera ab:n
Det reguljära uttrycket [Ll]abb?[1-7] kan användas för att hitta alla labbvarianter vi eftersökte ovan.
Det finns UNIX-kommandon som använder reguljära uttryck: egrep som letar efter ett reguljärt uttryck i en textfil, sed som kan byta ut valda delar av en fil (där delarna väljs ut med hjälp att ett reguljärt uttryck) awk som är ett programmeringsspråk som bygger på att vissa instruktioner ska utföras vid varje matchning av ett uttryck.
Pythonmodulen re har funktionalitet för reguljära uttryck. Exempel:
import re pattern="[Ll]abb?[1-7]" sometext="Lab5, labb 6, labb7 och lab8" print(re.findall(pattern,sometext)) # Utskriften blir ['Lab5', 'labb7']
Bakom kulisserna i re-modulen skapas automater som kan kontrollera om indata matchar det givna uttrycket.
Modellering av grafiska gränssnitt
Många problem kan modelleras med automater. Objektorienterad programmering lämpar sig väl för att implementera tillstånden.
Exempel:
I många grafiska gränssnitt kan man markera text genom att trycka ner musknappen och hålla den nedtryckt medan man drar musen över texten. Det här kan vi se som en automat med ett normaltillstånd och ett markeringstillstånd, där musknappstryck/släpp ger övergång mellan tillstånden.
Objektmodellering och tillståndsprogrammering kan man läsa mer om i kursen DD2385, Programutvecklingsteknik.
Är man särskilt intresserad av grafiska gränssnitt finns kursen DH2323, Datorgrafik med interaktion
Den som vill veta hur automater egentligen fungerar kan läsa Dilians kurs DD1372, Automata and languages (men den kräver en del andra förkunskaper).