Visa version
Visa
< föregående
Jämför
< föregående
Föreläsning 13 Repetition
- Saker vi inte hunnit med
- Hammingavstånd
- Mp3
- Användning av MD5 hashning, SHA m.m.
- Hashning datasäkerhet
- Syntax igen
- Om testning
- Dynamisk programmering
- Repetition
- Datalogi
- Abstraktion
- Datastrukturer
- Algoritmer
- Instuderingstips
- Tentan
I labb 8 och 9 ska du skriva ett program som kollar att molekyler som användaren matar in via tangentbordet följer en given syntax.
I labb 10 ska du bygga vidare på programmet från labb 6 så att det även skapar ett syntaxträd (och ritar upp det med hjälp av en färdig grafikmodul, molgrafik.py).
Syntaxträd
När man använder en syntax för att tolka text (indata, programkod etc) brukar man skapa ett syntaxträd som datastruktur för den parsade texten.
Ett syntaxträd är ett allmänt träd, där de inre noderna är icke-slutsymboler och löven slutsymboler.
Välkänt exempel:
Språket som består av meningar av typen
JAG VET ATT DU TROR ATT JAG VET OCH JAG TROR ATT DU VET ATT JAG TROR har följande syntax:
<Mening> ::= <Sats> | <Sats><Konj><Mening>
<Konj> ::= ATT | OCH
<Sats> ::= <Subj> <Pred>
<Subj> ::= JAG | DU
<Pred> ::= VET | TROR
Vi kan skapa ett syntaxträd för en given mening genom att parsa meningen och identifiera delarna. Exempel:
JAG VET
är en <Mening>, som i sin tur är en <Sats>, som är <Subj> följt av <Pred>, där <Subj> är JAG och <Pred> är VET.
Uppgift: Givet följande BNF-grammatik för vanliga taluttryck med operationerna + - * /.
<Uttryck> ::= <Term> | <Term> + <Uttryck> | <Term> - <Uttryck>
<Term> ::= <Faktor> | <Faktor> * <Term> | <Faktor> / <Term>
<Faktor> ::= TAL | -<Faktor> | (<Uttryck>)
Rita upp ett syntaxträd för uttrycket 2*(3+4*5).
Lösning:
|
*
/ \
2 ( )
|
+
/ \
3 *
/ \
4 5
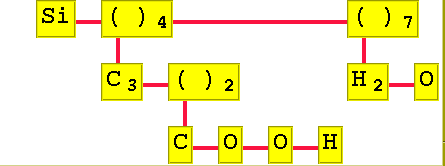
Syntaxträdet i labb7 ska representeras av ett allmänt träd där varje nod (motsvarar en ruta i bilden nedan) kan representeras med ett objekt av klassen Ruta nedan:
class Ruta:
def __init__(self):
self.atom = "( )"
self.num = 1
self.next = None
self.down = None
Molekylen Si(C3(COOH)2)4(H2O)7 får följande utseende:
Sist i laboration 7 ska du också beräkna molekylernas vikt. För att göra det ska du använda hashtabellen du skrev laboration 5!
Kattis
Kattis: Ett automatiskt system för rättning av labbar
Kattis började i form av Marvin, som användes för att rätta inlämningarna i programmeringstävlingskursen DD2458 (programmering och problemlösning under press), men används numera även i DD1352 (Algoritmer, Datastrukturer och Komplexitet) och DD2387 (Programsystemkonstruktion med C++) med flera.
Kattis är skrivet i en kombination av Python, PHP och SQL och körs på en Ubuntu-server. En specialbyggd säkerhetslösning används för att hindra fusk. All inskickad kod lagras också för att senare kunna kontrollera koden ifall det skulle behövas.
Den pedagogiska tanken med Kattis är att eleverna skall kunna sända in sin kod och snabbt få svar på huruvida koden fungerar. Kattis skall även ge eleverna övning i att söka efter buggar i koden. Kattis har utvecklats av:
- Fredrik Niemelä
- Gunnar Kreitz
- Per Austrin
Övriga som hjälpt till är:
- Johanna Eriksson
- Mattias de Zalenski
- Pehr Söderman
Hur ska jag göra?
- Följ länken: Kattis
- Logga in (längst upp till höger) med ditt KTH-id
- Välj "COURSES" i övre menyn
- Välj "tilda15" (långt ner i listan)
- Klicka på "I am a student taking this course and I want to register for it on Kattis."
- Välj "Problemlista".
Här finns två testproblem (hello och different) och labb 6 (formelkoll2) - Välj "SUBMIT" för att komma till inskickningssidan.
- Fyll i fälten "Problem ID" och "Language"
- Välj en fil (ditt python-program)
- Tryck på knappen "Skicka in"
- Uppdatera webbsidan för att få se Domarstatus.
Använd testproblemen för att lista ut hur Kattis fungerar innan du skickar in din lösning till labb6!
Indata
Programmen du skickar till Kattis ska läsa indata från stdin.
Det fungerar som att läsa från fil! Exempel:
from sys import stdin
from formelkollPaket import * #För att inte hela labben ska synas ;-)
def main():
#stdin = open("indata1.txt") #Lätt att ändra för att testa indata från fil
rad = stdin.readline()
while rad[0] != "#":
q = LinkedQ()
for tkn in rad:
q.put(tkn)
try:
readformel(q)
print("Formeln är syntaktiskt korrekt")
except Syntaxfel as felet:
rest = str(q).strip()
print(felet, "vid radslutet", rest)
rad = stdin.readline()
main()
Utdata
Utdata ska du skriva ut med print som vanligt.
print(x)
Syntaxfel
Definiera ditt eget särfall som en subklass till Exception. Du behöver inte göra egna metoder - allt som finns i Exception ärvs av din klass.
Exempel (Python 3):
class Syntaxfel(Exception):
pass
def readformel(q):
...
raise Syntaxfel("Felaktig gruppstart")
Repetition
Detta är en repetitionsföreläsning. Den täcker inte hela kursen, men är en översikt och snabbgenomgång.
Kursen heter Tillämpad datalogi. Mängden tillämpningar är obegränsad. All tillämpning bör motiveras - man måste kunna tala om varför man valt att göra på ett visst sätt.
Datalogi
Vad var datalogi nu igen?
Datalogi är läran om datastrukturer och algoritmer, dvs hur man kan organisera och hålla reda på data samt hur dessa data kan utnyttjas enligt en steg-för-steg-beskrivning för att (effektivt) lösa något problem.
Abstraktion
Ytterligare ett centralt begrepp i kursen är abstraktion. I Nationalencyklopedin står det så här:
- Abstrakt: "En föreställning är abstrakt om den syftar till att fånga det allmängiltiga hos företeelsen i fråga och bortse från eventuella tillfälligheter. Föreställningen om cirkelns begrepp är t.ex. en abstrakt föreställning till skillnad från föreställningen om en enskild cirkel."
- Abstrakt tänkande: "Abstrakt tänkande är tankeprocesser som grundar sig på abstrakta begrepp och allmänna principer och inte på enskilda föremål eller konkreta företeelser, och där olika begrepp kan sammanställas till nya helheter, i vilka oväsentliga delar utelämnats."
I datalogi:
- I definitionen av en abstrakt datatyp (ADT) anger man vilka operationer som finns (t ex insert(x), exists(x)), dvs man definerar ett gränssnitt.
- Vid konstruktion av algoritmen behöver man inte tänka på implementationen av datastrukturerna.
- Det här gör det lättare för programmerare att samarbeta i ett projekt:
- Den som skriver ADT:en kan ändra implementationen, så länge allt fungerar likadant.
- Den som använder ADT:en behöver inte bry sig om hur den är konstruerad, utan behöver bara förstå gränssnittet.
- Förenklar kodåtervinning (tänk på labbarna i kursen!).
Ett exempel: en abstrakt ordlista kan tex defineras med ett gränssnitt bestående av två operationer:insert(x), exists(x).
Ni har själva implementerat en sådan datastruktur på två olika sätt
- I labb 3 - med binärt sökträd
- I labb 5 del 2 - med en hashtabell
När ni sedan använde ordlistan i breddenförstsökningen i labb 4 så använde ni den abstrakt, utan att reflektera över hur den var implementerad.
Datastrukturer
Datastrukturer används för att lagra och använda data. I kursen har åtminstonde följande datastrukturer tagits upp:
- Små objekt för egendefinierade saker (t ex Noder av olika slag)
- Länkade listor bestående av noder med en next-pekare
- Vektor (pythons inbyggda lista)
- Stack (implementerad med en länkad lista)
- Kö (implementerad med en länkad lista)
- Allmänna träd (implementerade med noder med två pekare)
- Binära träd (implementerade med noder med två pekare)
- Hashtabeller (implementerade med en vektor)
- Booleska hashtabeller och bloomfilter
- Trappa/heap (implementerad med en vektor som tolkas som ett binärträd)
- Prioritetskön (implementerad med en trappa)
Vi har definerat dessa datastrukturer abstrakt - vi är överens om hur de bör funka. Dessutom har vi implementerat dem. Sedan har vi använt dem på ett abstrakt vis - utan att behöva bry oss om hur de var implementerade. I kursen ingår både och - att förstå hur de funkar och använda dem på ett abstrakt plan.
Algoritmer
Algoritmer används för att lösa problem. En algoritm utnyttjar en eller flera olika typer av datastrukturer och det är rätt datastruktur i kombination med rätt algoritm som gör algoritmen effektiv. I kursen har åtminstonde följande algoritmer tagits upp:
- Sökning, tex:
- Linjärsökning
- Binärsökning
- brute-force
- Grafgenomgång/sökning i graf, tex:
- Breddenförstsökning
- Djupetförstsökning
- Bästaförstsökning
- Fullständig trädgenomgång
- Rekursiva algoritmer, tex:
- Listrekursion
- Trädrekursion
- Binärträdssökning, -utskrift
- Rekursiv medåkning för syntaxkontroll
- Sortering, tex:
- Urvalssortering
- Insättningssortering
- Bubbelsortering
- Räknesortering (Distribution count)
- Radixsortering (Hålkortssortering)
- Damernaförstsortering
- Kvicksortering (Quicksort)
- Samsortering (Mergesort)
- Trappsortering (Heapsort)
- Hashning, med tillämpningar:
- En miljon sånger
- Data för atomer
- Bloomfilter
- MD5, SHA
- Textsökning, tex:
- KMP-automat för textsökning
- Boyer-Moore
- Rabin-Karp
- Reguljära uttryck
- Komprimeringsalgoritmer, tex
- Följdlängdskodning (RLE)
- Huffmankodning
- Lempel-Ziv-kodning (LZ), speciellt LZW
- Redundans
- paritetsbitar
- hammingavstånd
- Krypteringsalgoritmer, tex
- Transpositionschiffer
- Caesarchiffer
- rot13
- Bokchiffer
- One-time pad
- Key exchange
- RSA
Det finns också en mängd namnlösa småalgoritmer som ingår i de ovanstående. Givetvis är det viktigt att förstå hur ett binärt träd byggs upp innan man kan söka i det, hur en hashtabell eller en boolesk hashtabell fylls i innan sökning kan ske och så vidare. Hur man sätter in något i en datastruktur kan ju också beskrivas med en algoritm!
Algoritmer jämförs genom antalet operationer som måste utföras givet ett antal element eller mer grovt med komplexitetsberäkningar, där komplexiteten anges med en funktion av viss storleksordning, Ordo, O(f(N)). Ibland jämförs smartare algoritmer med en brute-force algoritm (som går igenom alla alternativ). Här är en på intet sätt uttömmande tabell över några algoritmer och deras tidskomplexitet. Kom ihåg att det inte räcker att kunna dessa utantill - man måste även kunna resonera om varför det är så, och när det inte gäller.
KomplexitetAlgoritmer
| O(n2) | enkla sorteringsalgoritmer, quicksort |
| O(n*log(n)) | mergesort, heapsort, quicksort |
| O(n) | linjärsökning, räknesortering |
| O(log(n)) | binärsökning, sökning och insättning i binärträd |
| O(1) | insättning och sökning i hashtabell |
| 1 | en addition, en multiplikation, en jämförelse |
När man anger ordoklassen behöver man bara ta med den största termen, och kan strunta i multplikation eller division med konstant, t ex är O(nlogn(n) + 155*log(n) - 1) = O(nlog(n)).
Man mäter komplexitet i enkla operationer (tex: en addition, en multiplikation eller en jämförelse). Vilken operation man mäter beror på vilken typ av algoritm det är frågan om. Exempelvis innehåller all någon form av jämförelse så där är det naturligt att räkna antal jämförelser snarare än aritmetik.
Man måste naturligtvis definera vad man menar med de i uttrycket ingående variablerna och vilka förutsättningar som gäller.
Samma algoritm har olika tidskomplexitet vid olika förutsättningar. Ofta (men inte alltid) är man intresserad av det värsta fallet och de förutsättningar som gör att algoritmen tar längst tid. Här är en tabell över hur lång tid det tar (hur många jämförelser det går åt) för att hitta ett värde i ett binärt sökträd i några olika fall:
Sökning i balanserat binärträdTidsåtgång
| Om det sökta finns, i bästa fall | 1 |
| Om det sökta finns, i värsta fall | log(n) |
| Om det sökta finns, i snitt | log(n)-1 |
| Om det sökta ej finns | log(n) |
Om man vet att det sökta finns och bara vill konstatera var i trädet det finns behöver man inte kontrollera den sista noden. Då blir värsta fallet: log(n)-1 och snittet ungefär: log(n)-2.
Men om insättningen i det binära trädet gick dåligt ligger alla värden i en tarm och då blir sökningen som i en enkellänkad lista:
Sökning i enkellänkad listaTidsåtgång
| Om det sökta finns, i bästa fall | 1 |
| Om det sökta finns, i värsta fall | n |
| Om det sökta finns, i snitt | n/2 |
| Om det sökta ej finns | n |
Om man vet att det sökta finns och bara vill konstatera var i listan det finns behöver man inte kontrollera den nedersta noden. Då blir värsta fallet: n-1 och snittet: (n-1)/2.
OBS. Oftast har man ingen aning om huruvida det sökta finns eller inte...
Instuderingstips
För varje datastruktur och algoritm gäller att åtminstonde kunna:
- Förstå
- Abstrakt: hur använder man den?
- Konkret: hur implementerar man den? (Kunna beskriva i ord.)
- Analysera
- Hur snabb/effektiv är den? Tidsomplexitet/minnesåtgång.
- Vad har den för fördelar/nackdelar? Begränsningar?
- När är den lämplig/olämplig, jämfört med andra algoritmer/datastrukturer?
Betygskriterier
För betyg E
ska du kunna avgöra vilken algoritm som löser ett givet problem, kunna beskriva algoritmen och demonstrera den steg för steg med givna data, samt implementera den. Motsvarande gäller för datastrukturer.
För betyg C
ska du ha uppfyllt kraven för betyg E, och dessutom ska du kunna jämföra algoritmer och datastrukturer och bedöma dessas lämplighet för ett givet problem. Här ställs också krav på tidsplanering.
För betyg A
ska du ha uppfyllt kraven för betyg C, och du ska dessutom kunna modifiera/kombinera algoritmer och datastrukturer för att lösa nya problem. Här ställs också höga krav på tydlighet i algoritmbeskrivningar.
Tentan
Mest problemfrågor, t ex:
- Demonstrera en algoritm för givna data.
- Visa hur en operation i en datastruktur fungerar för givna data.
- Beskriv en algoritm som löser ett givet problem.
- Uppskatta tidskomplexiteten för din algoritm.
- Berätta vilka algoritmer/datastrukturer från kursen som kan användas.
- Resonera om varför en viss algoritmen/datastrukturern är lämplig i sammanhanget.
Men också teorifrågor, t ex:
- Vilken tidskomplexitet har algoritmen xxx?
- Vad är viktigt att tänka på när en använder datastrukturen yyy?
Kom ihåg:
- Viktigt att motivera svaren!
- Viktigt att motiveringar är tydliga.
- Inte viktigt att skriva programkod, strukturerad text eller pseudokod går bra.
- Rita gärna, så blir det lättare för oss rättare.
Hjälpmedel
- Ett egenhändigt skrivet formelblad, en A4.
- Du får skriva precis vad du vill på fram- och baksidan.
- Du får inte ta med ett formelblad som någon annan har skrivit.
- Formelbladet ska lämnas in tillsammans med tentan.
- En valfri bok (tryckt - inte utskriven) om algoritmer/datastrukturer, t ex kursboken.
- Du får inte ta med föreläsningsanteckningar.
- Du får inte ta med extentor.
Tid och plats:
- Ordinarietentan ges fredag 23 oktober kl 08:00-12:00
- Omtenta torsdag 7 januari 2015 kl 14:00-18:00
Tentauppgift betyg C: Rekursiv bränsleåtgång
Bränsleåtgången per antal maskhålshopp som rymdvarelserna gör räknas ut med följande rekursiva metod. En tildastudent påpekar vänligt för rymdvarelserna att implementationen är onödigt ineffektiv.
def fuel(N): # N is nr of wormhole jumps
if N == 0 :
return 3000
if N == 1 :
return 2990
else:
return fuel(N-1) + fuel(N-2) - 3000
Gör följande:
- Ange bränsleåtgången för 6, 5, 4, 3, 2, 1 maskhålshopp
- Förklara vad som är ineffektivt med implementationen.
Tentauppgift betyg A: Silhuettproblemet
Om man på håll betraktar en stad i skymningen ser man inte dom enskilda byggnaderna utan bara silhuetten, den yttersta konturen, avteckna sig mot himlen. Hitta på en algoritm som givet varje byggnads kontur beräknar stadssilhuetten. 
Anta att alla byggnader står påx-axeln, är rektangulära och beskrivs av tripplar(left, height, right) därleft är vänsterväggensx-koordinat,right är högerväggensx-koordinat ochheight är höjden (y-koordinat).
Inmatningen består avn stycken tripplar, ordnade i stigande värden på vänsterväggar, och utmatningen ska vara en rad med x,y-koordinater som från vänster till höger beskriver silhuetten.x-värdena anger var påx-axeln silhuetten går vertikalt ochy anger på vilken höjd silhuetten fortsätter efterx-värdet. Den sistay-koordinaten är alltid noll eftersom alla byggnader står påx-axeln.
Exempel: Om n=8 och inmatningen är
(1,11,5) (2,6,7) (3,13,9) (12,7,16) (14,3,25) (19,18,22) (23,13,29) (24,4,28)
så blir utmatningen
x= 1 y= 11
x= 3 y= 13
x= 9 y= 0
x= 12 y= 7
x= 16 y= 3
x= 19 y= 18
x= 22 y= 3
x= 23 y= 13
x= 29 y= 0