Föreläsning 12 Kryptering, datasäkerhet

Kryptering och datasäkerhet

Läs i boken: kap 3.4.3
Kryptering:

Transpositionschiffer
Cesarchiffer
Bokchiffer
One-time pad
Säker nyckelöverföring
RSA

Datasäkerhet
Lösenord
Validera data
Dekompilera kod

Kryptering

Att kryptera ett meddelande innebär att vi kodar det så att det blir oläsligt för alla utom den som vet hur man dekrypterar det. Kryptering används i alla sammanhang där man har anledning att hålla något hemligt, t ex vid överföring av kontokortsnummer över internet eller när man vill skicka lägesrapporter från diktaturer.

Olika former av kryptering har använts så länge man har velat ha skriftliga hemligheter. Redan dom gamla grekerna hade flera system för kryptering.

Rollista:

Alice som vill skicka ett meddelande till Bob
Bob som vill få meddelandet från Alice (oläst)
Eve (av engelskans eavesdrop - tjuvlyssna) som försöker avkoda meddelandet

Transpositionschiffer

I det antika Grekland användes en scytale - en dekrypteringspinne för att avkoda hemliga meddelanden skrivna på en remsa skinn. Avsändaren (Alice) och mottagaren (Bob) har varsin pinne av samma diameter. Avsändaren lindar skinnremsan som en spiral runt pinnen och skriver sitt meddelande längs med pinnen. Remsan blir då obegriplig tills den hamnar i mottagarens händer.

Samma effekt kan vi få genom att skriva meddelandet i en mxn-matris och bilda det kodade meddelandet genom att ta varje kolumn i texten. Den som känner till matrisens storlek kan lätt avkoda det. Man brukar skippa mellanslag och skiljetecken för att göra det svårare att knäcka koden.

JAGGÖ
MMERP
ENGAR
NAIDE
NGAML
AEKEN

kodas alltså som:

JMENNAAMNAGEGEGIAKGRADMEÖPRELN

Caesarchiffer

Julius Caesar lär ha använt denna metod:
A byts mot D
B byts mot E
C byts mot F
osv.

En variant är rot13 där man förskjuter varje bokstav 13 steg. Hamnar man utanför alfabetet roterar man runt till början igen.

def rot13(meddelande):
    alfabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
    kod = ""
    for bokstav in meddelande:
        index = (alfabet.find(bokstav) + 13) % 26
        kod = kod + alfabet[index]
    return kod

Om vi skippar ÅÄÖ får vi ett alfabet som består av 26 tecken, vilket innebär att vi kan använda samma funktion för dekryptering!

rot13("HEMLIGHETER") blir URZYVTURGRE

rot13("URZYVTURGRE") blir HEMLIGHETER

Ännu hemligare blir det om vi slumpar fram en mappning istället för att flytta fram ett visst antal steg.

ABCDEFGHIJKLMNOPQRSTUVWXY
|||||||||||||||||||||||||
FSXNVDQBCULRHKTPAOMWJEIGY

Alla dessa chiffer är dock enkla att knäcka för Eve, som har statistik över hur ofta varje bokstav förekommer i det aktuella språket. Så här ser det ut för svenska:

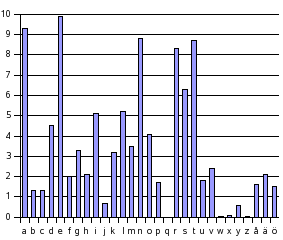
Bokchiffer

I Sir Arthur Conan Doyles The Valley of Fear knäcker Sherlock Holmes ett bokchiffer.

Det är ett enkelt men mycket effektivt chiffer där man använder en bok som nyckel. Man letar rätt på ordet i boken och skriver ner sidnummer samt ordets nummer på sidan, t ex

534 13 127 220 10 109 220 129

Den ena siffran anger sidan och den andra anger vilket ord på sidan det är. (Man kan använda bokstäver istället för ord, men då ska det vara en tjock bok.) Alice och Bob måste i förväg ha kommit överens om vilken bok det gäller utan att Eve hör).

One-time pad

One-time pad är en oknäckbar krypteringsmetod som använder sig av en slumpad nyckel.

Givet ett meddelande på binär form:

Slumpa fram en nyckel med lika många binära siffror som meddelandet har
Gör bitvis xor mellan meddelandet och nyckeln

Det resulterande kodade meddelandet kan bara dekrypteras av den som har den slumpade nyckeln.

Alice och Bob måste ha varsitt exemplar av en "pad" (ett block) med slumpade siffror, som inte Eve har tillgång till.
Alice använder första sidan i sitt block för att kryptera ett meddelande och river sedan av första arket och äter upp det.
Bob dekrypterar med sin första sida, river av och eldar upp arket.

Säker nyckelöverföring

Alice vill skicka ett exemplar av blocket till Bob utan att Eve (som jobbar som brevbärare) kan kopiera det. Hur ska hon göra?

Alice lägger blocket i en ibrottssäker låda och sätter sitt A-lås på det. Endast hon själv har A-nyckeln.
Hon skickar lådan till Bob (Eve kan inte låsa upp den).
Bob kan inte öppna lådan ännu. Han sätter på sitt B-lås. Endast Bob har B-nyckeln.
Han skickar tillbaka lådan till Alice.
Alice låser upp A-låset och plockar bort det. Nu är lådan enbart låst med B-lås.
Hon skickar lådan till Bob, som låser upp den och får sitt block.

Asymmetrisk kryptering

Ett problem med många chiffer är att man måste berätta för mottagaren hur hon ska dechiffrera meddelandet. Hur är man säker på att den viskningen inte blir avlyssnad?

Asymmetrisk kryptering (RSA) förutsätter nyckelpar. En publik och en privat nyckel hos vardera part. Man krypterar med mottagerens publika nyckel och signerar med sin egen privata nyckel. Mottagaren dekrypterar med sin privata nyckel och autentiserar med sändarens publika nyckel.

Bob har en publik och privat nyckel. Han lägger upp den publika på sin webbsida där alla kan se den (även Eve). Alice krypterar ett meddelande med Bobs publika nyckel och skickar meddelandet till Bob. Eve kan inte läsa det krypterade meddelandet, men Bob kan dekryptera med sin privata nyckel.

Vid symmetrisk kryptering har sändare och mottagare samma krypteringsnyckel. Det går i regel mycket fortare än asymmetrisk kryptering. Standarden idag är AES, tidigare var det DES.

RSA

Krypteringsalgoritmen RSA (döpt efter Ron Rivest, Adi Shamir och Leonard Adleman som först publicerade den) är ett exempel på asymmetrisk kryptering. Du har en offentlig nyckel och en privat nyckel. Den offentliga nyckeln delar du ut till alla, så att dom kan kryptera meddelanden och skicka till dig, men det är bara du som kan dekryptera med hjälp av den privata nyckeln.

Först måste vi beräkna nycklarna:

Välj två stora primtal, p och q.
Beräkna n = p*q.
Beräkna f = (p-1)*(q-1).
Välj e så att det inte har några gemensamma faktorer med f (dvs gcd(e,f) ska bli 1).
Beräkna d som den multiplikativa inversen till e modulo f, dvs så att e*d modulo f = 1.

e och n är offentliga, medan d är privat. Själva krypteringen går till så att man först konverterar meddelandet till ett tal (t ex genom att konkatenera ASCII-koderna). Man delar upp det i lagom stora delar som vi kallar m₁, m₂ osv.

Sedan beräknar vi m_i^e modulo n för att få de kodade delarna c_i.

Den som vill dekryptera måste känna till d, och kan då få ut det ursprungliga meddelandet genom att beräkna c_i^d modulo n för varje c_i.

På University of Illinois har man gjort en demo av RSA, prova gärna!

För att knäcka RSA måste man faktorisera n, dvs lista ut vilka de två stora primtalen p och q är. Det finns ännu ingen algoritm som kan göra detta i polynomisk tid, dvs O(L^k) där L är längden av primtalet och k är en godtycklig konstant, vilket innebär att beräkningen tar för lång tid för att vara praktiskt användbar. Därför räknar man med att RSA i nuläget är oknäckbar för tillräckligt stora primtal.

Ovannämnda algoritmer är publika och man kan matematiskt verifiera att de fungerar. Det som är hemligt är nycklarna. Att hemlighålla algoritmen (security by obscurity) bör betraktas med skepsis. Under 2013 läckte Edward Snowden hemligt material i huvudsak från amerikanska NSA vilket bekräftat bilden av att algoritmerna i huvudsak håller men att det finns mängder med andra säkerhetsproblem.

Datasäkerhet

Lösenord

Lösenord bör sparas saltade och hashade.

Exempelvis skulle en lösenordsfunktion:

def testaHemligtPassword( password ):
   if password == "123aabbccdd" :
       return True
   else: 
       return False

kunna skrivas så här:

def dunkeltPasswordsTest(password):
   hårdkodat_salt = "123£"!#¤!..."
   hårdkodat_saltat_och_hashat_lösen = "312sd3$£$#!SESD..."

   hashat_password = hashfunc( password + hårdkodat_salt)
   if hashat_password == hårdkodat_saltat_och_hashat_lösen :
      return True
   else:
      return False

Givet koden är det svårt att gissa lösenordet. Eftersom en hashfunktion kan ge samma värde för två helt olika indata (krock) så går det inte att, givet hashvärdet, lista ut vilket det ursprungliga värdet var.

Det finns bra och dåliga lösenord. I mars 2013 anordnade nättidningen Ars Technica en tävling att gissa hashade lösenord. Artikeln beskriver hur lösenordsgissningsalgoritmerna jobbar. Bl.a. används befintliga lösenord som algoritmen hakar på suffix och prefix. Bruce Schneier är en säkerhetsexpert som bloggar om datasäkerhet och ger en del råd om lösenord.

Validera indata

Ett användarvänligt program berättar för användaren om indata är på fel format så att hen har chans att rätta till det. Men det finns ytterligare skäl till att validera inmatning innan den skickas vidare till programmet - det är en möjlig säkerhetsrisk.

Kontrollera t ex:

Indatas längd
Datatyp
Filformat (inte bara ändelsen)

Dekompilera kod

Under 2014 publicerades två artiklar (1, 2) som kunde visa att det går att skriva kod som inte går att hacka. Definitionen på ej hackningsbar skulle vara att den som har tillgång till källkoden inte vet mer än den som har den kompilerade koden. För den senare fungerar koden som en svart låda (black box).

Mer att läsa

I Simon Singhs kodbok finns tio chiffreringsuppgifter av stigande svårighetsgrad. De första att knäcka alla tio var ett lag med dåvarande/blivande doktorander i teorigruppen TCS på CSC, Här är deras berättelse om hur det gick till.

En fortsättningskurs som bland annat handlar om tillämpningar av kryptering är DD2395 Datasäkerhet. Där får man också lära sig om t ex virus och datajuridik.

Säkerhetsaspekter tas även upp i kursen DD1334 Databasteknik som vissa av er läser redan i vår.

Vi har förstås också kursen DD2448 Kryptografins grunder (men den kräver att man läst DD1352 ADK först).