Hoppa till huvudinnehållet
Till KTH:s startsida

[Paper 20] The Interior Volumes of Black Holes

This is a short non-technical summary of my paper arXiv:1503.01092 [gr-qc]. I plan to write a longer version to tell all the interesting stories, but that's for another time...

The simplest black hole solution to Einstein's general relativity was found by Karl Schwarzschild, in only a few months after Einstein's publication of his theory [the fact that the solution describes a black hole would take some time to be fully understood]. Like a star, a black hole is spherical. The surface of a black hole is called an "event horizon", which is not really a physical surface, but marks the boundary of no return -- any object that falls through the horizon will be doomed to hit the black hole singularity, where spacetime curvature becomes unbounded. 

A Schwarzschild black hole is therefore a sphere of surface area tex:\displaystyle 4\pi r_h^2, where tex:\displaystyle r_h is the "Schwarzschild radius" that defines the event horizon [specifically, tex:\displaystyle r_h=2GM/c^2. Usually one works in the units tex:\displaystyle G=c=1]. It is therefore tempting to think that its volume has to be tex:\displaystyle 4\pi r_h^3/3. This would be misleading. In fact there is no unique volume that one can assign to a black hole. [For people who know some general relativity: because 3-volumes depend on the choice of spacelike hypersurfaces.]

Nevertheless, recently Christodoulou and Rovelli showed that it makes sense to talk about the "largest volume" that can be bounded by the event horizon [arXiv:1411.2854 [gr-qc]]. They showed that even though a Schwarzschild black hole looks the same forever to an outside observer [this is a statement without considering Hawking radiation (quantum effect) that would shrink the black hole], its volume actually gets larger with time.

Untitled.png

A sphere with radius tex:\displaystyle R has area tex:\displaystyle 4 \pi R^2 and volume tex:\displaystyle 4\pi R^3/3 ; a black hole with Schwarzschild radius tex:\displaystyle r_h has area tex:\displaystyle 4\pi r_h^2 but its interior volume grows with time tex:\displaystyle v, although its area does not change! [Technically, it grows asymptotically linearly in advanced time tex:\displaystyle v]

________________________________________________________________________

Still, such notion of volume conforms to our intuition that the bigger the area is the larger its volume will be. [In more precise terms, the volume is a monotonically increasing function of surface area.] For example, a sphere of area tex:\displaystyle A has volume that is proportional to tex:\displaystyle A^{3/2}, so for larger area the volume is also larger. This is also true for a black hole that is rotating [like the one in the movie Interstellar ], as shown by Bengtsson and Jakobsson [arXiv:1502.01907 [gr-qc]].

However, I showed that this is not always true. This is perhaps not surprising with hindsight, after all our intuition does not work very well when spacetime is curved. In any case it is nice to see some explicit examples in which the volumes behave differently than what we would normally expect. For example, there is a class of black holes, all with the same mass, yet if we wait long enough, their interior volumes all become [almost] identical, regardless of their surface areas. In yet another class of solutions, for two black holes of the same mass, the one that has a larger surface area actually bounds a smaller volume, which is totally counter-intuitive. 

The lesson is that, general relativity is a geometric theory in which curvature plays important role. It would be a mistake to ignore geometry and rely on our flat space intuition when dealing with gravity. 

________________________________________________________________________

Some semi-technical details 

One of the cases I investigated concerns spherical black holes in 5-dimensional spacetime, so its "area" is 3-dimensional and its "volume" 4-dimensional. It is hard to imagine higher dimensional objects. However we can imagine constructing them starting from lower dimensional objects.

To show how this works, let's consider a usual sphere. [When mathematicians talk about spheres, they mean hollow spheres. A solid one is usually called a ball.]  One can construct a sphere starting from a solid disk, and gluing up its boundary to a point. [In the language of topology, we identify all the points on the boundary]. Essentially this "wraps up" the disk.
Similarly we can take a solid ball and glue up its surface to form a 3-dimensional [hollow] sphere, tex:\displaystyle S^3. [Note that the usual sphere is two-dimensional.]

Untitled2.png

In topology there is an interesting object called a "lens space". The simplest type of lens space is constructed as follows. Take a solid ball and divide it in half, the equator is then subdivided by the points tex:\displaystyle \{x_0, x_1, \cdots, x_{p-1}\}. Join these points with the north and south poles as shown in the following figure. Now twist the upper hemisphere by tex:\displaystyle 2\pi/p-radian. Finally, glue up all the upper "triangles" with their corresponding lower partners. This is the lens space tex:\displaystyle S^3/\Bbb{Z}_p. 

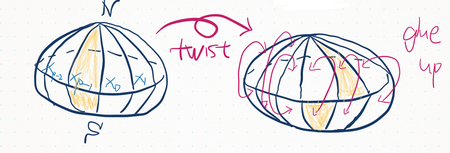
Untitled3.png

Black hole horizons with lens space topology can be constructed. A class of such black holes have the property we mentioned above: with fixed mass, if we increase the integer tex:\displaystyle p, the horizon area of such a "black lens" decreases. However, its volume increases! More details in the paper itself [arXiv:1503.01092 [gr-qc]]. 

Profilbild av Yen Chin Ong

Portfolio