Hoppa till huvudinnehållet
Till KTH:s startsida

Time-causal and time-recursive receptive fields

When modelling temporal operations on video data or other types of time-dependent signals, a fundamental constraint originates from the fact that the future cannot be accessed. For off-line processing of pre-recorded video data, the use of non-causal receptive fields based on Gaussian derivatives or Gabor functions can in some cases be sufficient. When operating on video data in a real-time setting or when modelling biological vision, the constraint of temporal causality does, however, need to be taken into explicit account.

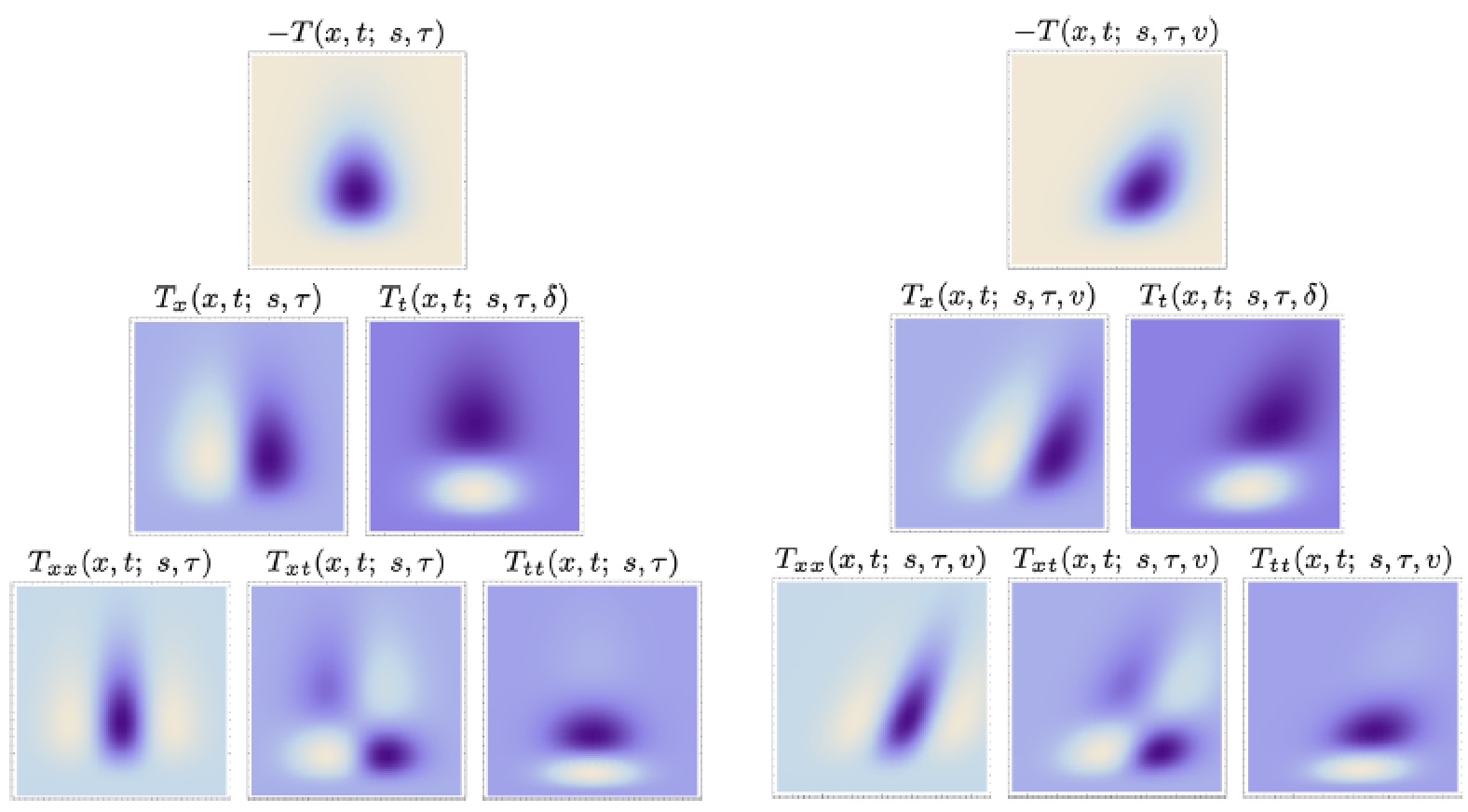
To address this problem, we have developed a principled framework for time-causal spatio-temporal receptive fields to be used as primitives for video analysis in a corresponding way spatial receptive fields based on Gaussian derivatives are used as primitives for spatial tasks in computer vision:

  • Lindeberg (2016) "Time-causal and time-recursive spatio-temporal receptive fields", Journal of Mathematical Imaging and Vision 55(1): 50-88. (Download PDF)
  • Lindeberg (2015) "Separable time-causal and time-recursive spatio-temporal receptive fields", Proc. SSVM2015: Scale-Space and Variational Methods in Computer Vision, (Lege-Cap Ferret, France), Springer LNCS 9087: 90-102. (Download PDF)

The temporal smoothing operation in this framework is based on a temporal kernel called the time-causal limit kernel, which permits scale covariance and scale invariance in a time-causal and time-recursive setting, and which is a novel theoretical construction. The temporal processing stage in this model is also time-recursive, with the attractive property that the temporal multi-scale representation by itself serves as a sufficient memory of the past, without need for additional temporal buffering, such as a video recording of the past.

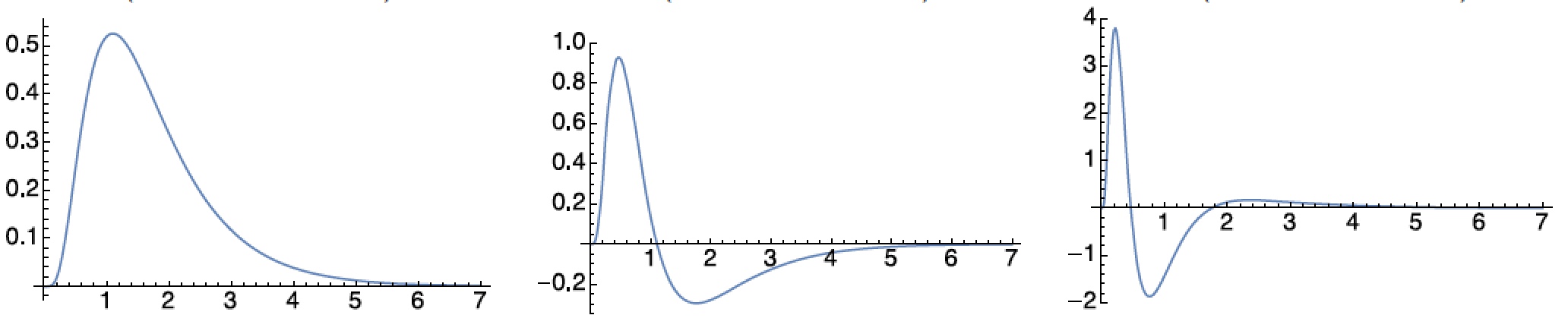
The time-causal limit kernel and its temporal derivatives obey several structurally similar properties over a time-causal temporal domain as the Gaussian kernel and its derivatives obey over a non-causal temporal domain. Specifically, the time-causal limit kernel allows for the formulation of a principled theory for temporal scale selection over a time-causal temporal domain:

  • Lindeberg (2017) "Temporal scale selection in time-causal scale-space", Journal of Mathematical Imaging and Vision, 58(1): 57-101. (Download PDF)

 

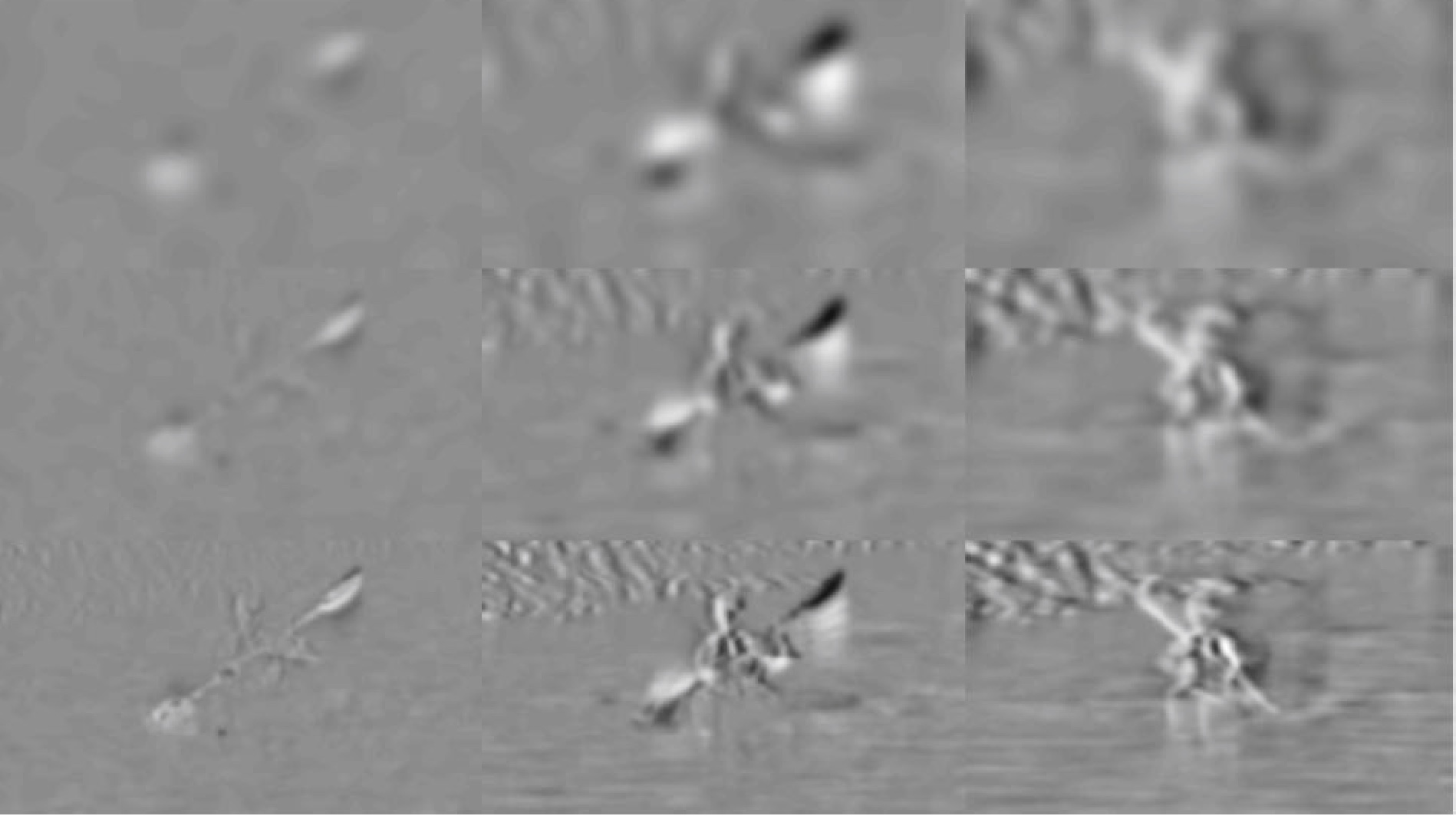
This theory does also extend to temporal scale selection and joint spatio-temporal scale selection in video data and does in this way provide a principled approach for processing spatio-temporal image structures over multiple spatio-temporal scales:

  • Lindeberg (2018) "Spatio-temporal scale selection in video data", Journal of Mathematical Imaging and Vision, 60(4): 525-562. (Download PDF)
  • Lindeberg (2018) "Dense scale selection over spatial, temporal and spatio-temporal domains", SIAM Journal on Imaging Sciences, 11(1): 407–441. (Download PDF)
  • Lindeberg (2017) "Spatio-temporal scale selection in video data", Proc. SSVM 2017: Scale-Space and Variational Methods in Computer Vision, (Kolding, Denmark), Springer LNCS 10302: 3-15. (Download PDF)

As a first application of using the receptive fields in this model as primitives for video analysis, we have developed a family of video descriptors based on regional statistics of spatio-temporal receptive field responses and evaluated this approach on the problem of dynamic texture recognition:

  • Jansson and Lindeberg (2018) "Dynamic texture recognition using time-causal and time-recursive spatio-temporal receptive fields", Journal of Mathematical Imaging and Vision, 60(9): 1369-1398. (Download PDF)
  • Jansson and Lindeberg (2017) "Dynamic texture recognition using time-causal spatio-temporal scale-space filters", Proc. SSVM 2017: Scale-Space and Variational Methods in Computer Vision, (Kolding, Denmark), Springer LNCS 10302: 16-28. (Download PDF)

The experimental evaluation demonstrates competitive performance compared to state-of-the-art. These results support the descriptive power of this family of time-causal spatio-temporal receptive fields and point towards the possibility of designing a wide range of video analysis methods based on these time-causal spatio-temporal primitives.

Profilbild av Tony Lindeberg