Complex numbers in rectangular and polar form. Basic geometry and topology the the complex plae and on the Riemann sphere. Holomorphic, meromorphic and harmonic functions. Conformal mappings. Taylor and Laurent series. Radius of convergence and termwise differentiation and integration of power series. Classification of singularities. Poles and zeros, the argument principle and Rouchés theorem. Liouvilles theorem with applications. Differentiation and integration in the complex plane. Cauchy- Riemann equations. Cauchys theorem and Cauchy's integral formula with corollaries. The maximum principle. Residues. Applications to, for example, transform theory, heat conduction and electricity theory.
SF1691 Complex Analysis 7.5 credits
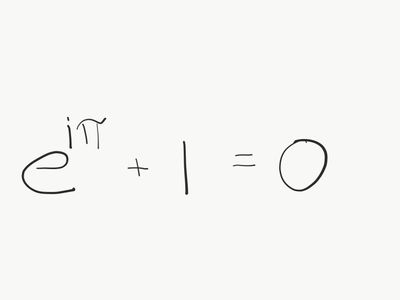
Complex analysis deals with functions of a complex variable, especially derivatives and integrals of such functions. Holomorphic funktions, i.e. functions that are differentiable in a complex sense, have a number of interesting properties and applications. It turns out that the so-called imaginary number i is very useful in investigating phenomena in our real reality. This course will be taught in Swedish. Information about the course round spring 2022 is available on canvas: https://kth.instructure.com/courses/31918
Information per course offering
Information for Spring 2025 Start 14 Jan 2025 programme students
- Course location
KTH Campus
- Duration
- 14 Jan 2025 - 2 Jun 2025
- Periods
- P3 (3.7 hp), P4 (3.8 hp)
- Pace of study
25%
- Application code
60178
- Form of study
Normal Daytime
- Language of instruction
Swedish
- Course memo
- Course memo is not published
- Number of places
Places are not limited
- Target group
- No information inserted
- Planned modular schedule
- [object Object]
- Schedule
- Part of programme
Degree Programme in Electrical Engineering, åk 2, Conditionally Elective
Degree Programme in Electrical Engineering, åk 3, Conditionally Elective
Degree Programme in Engineering Mathematics, åk 2, Conditionally Elective
Degree Programme in Engineering Mathematics, åk 3, Optional
Degree Programme in Engineering Physics, åk 3, Optional
Master's Programme, Applied and Computational Mathematics, åk 1, Optional
Master's Programme, Systems, Control and Robotics, åk 1, Recommended
Master's Programme, Systems, Control and Robotics, åk 1, LDCS, Conditionally Elective
Master's Programme, Systems, Control and Robotics, åk 2, Recommended
Master's Programme, Systems, Control and Robotics, åk 2, LDCS, Conditionally Elective
Contact
Course syllabus as PDF
Please note: all information from the Course syllabus is available on this page in an accessible format.
Course syllabus SF1691 (Autumn 2019–)Headings with content from the Course syllabus SF1691 (Autumn 2019–) are denoted with an asterisk ( )
Content and learning outcomes
Course contents
Intended learning outcomes
After the course the student should be able to
- explain the meaning of basic concepts, theorems and methods within the parts of complex analysis described by the course content
- use concepts. theorems and methods to solve and present solutions to problems within the parts of complex analysis described by the course content,
in order to solve applied problems and to communicate with the help of mathematical language, even in other contexts.
For higher grades, the student should in addition be able to
- explain how different theorems and concepts are connected and deduce relationships from the given theorems.
Literature and preparations
Specific prerequisites
Completed basic course SF1626 Calculus in Several Variable or SF1674 Multivariable Calculus.
Equipment
No information inserted
Literature
The course literature is announced on the course webpage four week before the start of the course.
Examination and completion
If the course is discontinued, students may request to be examined during the following two academic years.
Grading scale
A, B, C, D, E, FX, F
Examination
- TEN1 - Exam, 7.5 credits, grading scale: A, B, C, D, E, FX, F
Based on recommendation from KTH’s coordinator for disabilities, the examiner will decide how to adapt an examination for students with documented disability.
The examiner may apply another examination format when re-examining individual students.
The examiner decides, in consultation with KTHs Coordinator of students with disabilities (Funka), about any customized examination for students with documented, lasting disability. The examiner may allow another form of examination for re-examination of individual students.
Opportunity to complete the requirements via supplementary examination
No information inserted
Opportunity to raise an approved grade via renewed examination
No information inserted
Examiner
Ethical approach
- All members of a group are responsible for the group's work.
- In any assessment, every student shall honestly disclose any help received and sources used.
- In an oral assessment, every student shall be able to present and answer questions about the entire assignment and solution.
Further information
Course room in Canvas
Registered students find further information about the implementation of the course in the course room in Canvas. A link to the course room can be found under the tab Studies in the Personal menu at the start of the course.
Offered by
Main field of study
Technology
Education cycle
First cycle
Add-on studies
No information inserted